Calcul de la taille optimale d’un échantillon
Dans le cadre d’échantillonnage avec une méthode aléatoire, plus la taille de l’échantillon est grande, plus l’analyse sera précise. Ce qui parait logique. Mais la proportionnalité n’est pas vrai. L’analyse ne sera pas 2 fois plus précise, si votre échantillon est 2 fois plus important.
Il est important d’appréhender le fait que la taille de l’échantillon n’est pas en lien avec la taille de la population mère (ou très peu).
La détermination de la taille de l’échantillon est donc une étape importante avant toute enquête, qui est l’occasion d’arrêter la précision de l’analyse (souvent en fonction du budget alloué …).
Il existe 2 approches pour calculer la taille d’un échantillon :
- A partir d’une proportion, on peut calculer la taille de l’échantillon à partir de cette formule :
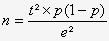
n = taille de l’échantillon attendu.
t = niveau de confiance déduit du taux de confiance (traditionnellement 1,96 pour un taux de confiance de 95%) – loi normale centrée réduite.
p = proportion estimative de la population présentant la caractéristique étudiée dans l’étude. Lorsque cette proportion est ignorée, une pré-étude peut être réalisée ou sinon p = 0,5 sera retenue.
e = marge d’erreur (traditionnellement fixée à 5%). - A partir d’une moyenne, il nous faut une première estimation de l’écart type afin de pouvoir ajuster l’échantillon en fonction de la précision des résultats qu’il procure et et du niveau d’analyse attendu :
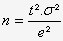
n = taille de l’échantillon attendu.
t = niveau de confiance déduit du taux de confiance (traditionnellement 1,96 pour un taux de confiance de 95%) – loi normale centrée réduite.
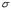 = écart type estimé de la moyenne du critère étudié.
= écart type estimé de la moyenne du critère étudié.
e = marge d’erreur.
